Pythagorean identity of Sine and Cosine functions

Formula

$\sin^2{\theta}+\cos^2{\theta} \,=\, 1$

The sum of the squares of sine and cosine functions at an angle equals to one is called the Pythagorean identity of sine and cosine functions.

Introduction

The sine and cosine are two functions in trigonometry. They have a direct relationship between them in square form but it represents the Pythagorean theorem. Hence, the relationship between sine and cosine functions in square form is called the Pythagorean identity of sine and cosine functions.

1. $\Delta BAC$ is a right triangle and its angle is denoted by theta.
2. The sine and cosine functions are written as $\sin{\theta}$ and $\cos{\theta}$ respectively.
3. Their squares are mathematically written as $\sin^2{\theta}$ and $\cos^2{\theta}$ respectively.

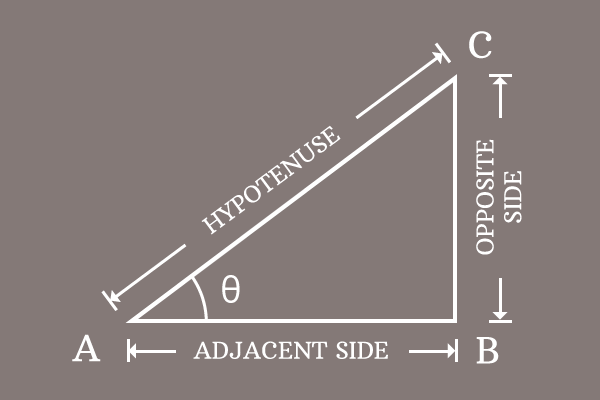
The sum of them is equal to one and it is called the Pythagorean identity of sine and cosine functions.

$\sin^2{\theta}+\cos^2{\theta} \,=\, 1$

Popular forms

The Pythagorean identity of sine and cosine functions is also written popularly in two other forms.

1. $\sin^2{x}+\cos^2{x} \,=\, 1$
2. $\sin^2{A}+\cos^2{A} \,=\, 1$

Remember, the angle of right triangle can be denoted by any symbol but the relation between sine and cosine functions should be expressed in that symbol.

Proof

Learn how to derive the Pythagorean identity of sine and cosine functions in mathematical form by geometrical method.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.