Proof of Pythagorean identity of Secant and Tangent functions

In fact, the Pythagorean identity of secant and tan functions is proved mathematically in trigonometry by the geometrical method. Now, let us learn how to derive the proof of the Pythagorean identity for the secant and tangent functions.

Write the relation between sides of the triangle

Draw a right triangle. It is considered as $\Delta BAC$ and its angle is represented by theta.

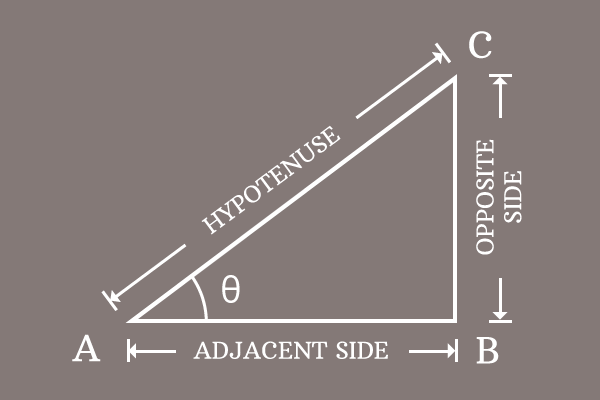
In this triangle, $\overline{BC}$, $\overline{AB}$ and $\overline{AC}$ are the opposite side, adjacent side and the hypotenuse respectively, and their respective lengths are written as $BC$, $AB$ and $AC$ mathematically.

As per the Pythagorean theorem, write the relation between the three sides of the right triangle in mathematical form.

${AC}^2 = {AB}^2+{BC}^2$

Remember this equation in your mind and it will be used for deriving the Pythagorean identity of secant and tan functions.

Express the sides in trigonometric functions

According to the right triangle $BAC$, let us try to write the lengths of the sides in terms of the secant and tan functions. Firstly, we have to express the secant and tan functions in their ratio form for doing it.

$\sec{\theta} \,=\, \dfrac{AC}{AB}$

$\implies$ $AC = AB \times \sec{\theta}$

$\tan{\theta} \,=\, \dfrac{BC}{AB}$

$\implies$ $BC = AB \times \tan{\theta}$

Express the equation in trigonometric form

We have already derived the lengths of the opposite site and hypotenuse in trigonometric functions in the above step.

1. $AC = AB \times \sec{\theta}$
2. $BC = AB \times \tan{\theta}$

Now, let us substitute them in the equation, which represents the relationship between then lengths of the sides of the right triangle.

${AC}^2 = {AB}^2+{BC}^2$

$\implies$ $(AB \times \sec{\theta})^2 = {AB}^2+(AB \times \tan{\theta})^2$

The terms in both sides of the equation can be simplified by the power rule of a product.

$\implies$ $(AB)^2 \times (\sec{\theta})^2$ $\,=\,$ ${AB}^2+(AB)^2 \times (\tan{\theta})^2$

$\implies$ ${AB}^2 \times \sec^2{\theta}$ $\,=\,$ ${AB}^2+{AB}^2 \times \tan^2{\theta}$

$\implies$ ${AB}^2 \times \sec^2{\theta}$ $\,=\,$ ${AB}^2 \times 1+{AB}^2 \times \tan^2{\theta}$

$AB^2$ is a common factor in the expression of the right hand side of the equation. So, it can be taken out common from them by the factorization.

$\implies$ ${AB}^2 \times \sec^2{\theta}$ $\,=\,$ ${AB}^2 \times (1+\tan^2{\theta})$

$\implies$ $\sec^2{\theta}$ $\,=\,$ $\dfrac{{AB}^2 \times (1+\tan^2{\theta})}{{AB}^2}$

$\implies$ $\sec^2{\theta}$ $\,=\,$ $\require{cancel} \dfrac{\cancel{{AB}^2} \times (1+\tan^2{\theta})}{\cancel{{AB}^2}}$

$\implies$ $\sec^2{\theta}$ $\,=\,$ $1+\tan^2{\theta}$

$\,\,\, \therefore \,\,\,\,\,\,$ $\sec^2{\theta}-\tan^2{\theta} \,=\, 1$

Therefore, it is proved that the subtraction of tan squared of an angle from the square of secant of angle is equal to one. It is called as the Pythagorean identity of secant and tan functions.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.