Reciprocal identity of Cot function

Formula

$\tan{\theta} \,=\, \dfrac{1}{\cot{\theta}}$

Proof

Cotangent is a ratio of lengths of adjacent side to opposite side and the tangent is a ratio of lengths of opposite side to adjacent side. Actually, the cot and tan functions are reciprocal functions mutually. So, the reciprocal of cot of angle equals to tan of angle.

$\Delta QPR$ is a right triangle and its angle is denoted by theta ($\theta$).

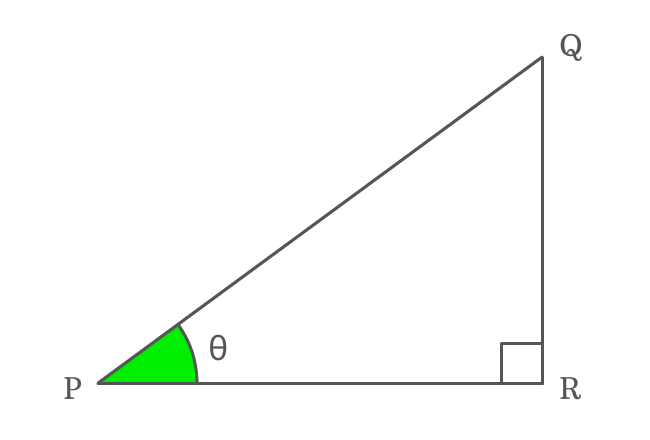
Write cotangent in its ratio form

Express cotangent of angle theta ($\cot{\theta}$) in its ratio form.

$\cot{\theta} \,=\, \dfrac{PR}{QR}$

Write Tangent in its ratio form

Similarly, write tan of angle theta ($\tan{\theta}$) in its ratio form.

$\tan{\theta} \,=\, \dfrac{QR}{PR}$

Relation between Co-tangent and Tangent

Lastly, write the value of tan function in ratio form into reciprocal form for deriving the relation between cot and tan functions in trigonometry.

$\implies \tan{\theta} \,=\, \dfrac{1}{\dfrac{PR}{QR}}$

$\,\,\, \therefore \,\,\,\,\,\,$ $\tan{\theta} \,=\, \dfrac{1}{\cot{\theta}}$

Therefore, it is proved successfully that the reciprocal of cot function is equal to tan function and it is used as a formula in mathematics.

Note

The angle of a right triangle can be denoted by any symbol but the reciprocal identity of cot function must be expressed in terms of the respective angle.

For example, if $x$ represents angle of right triangle, then

$\tan{x} \,=\, \dfrac{1}{\cot{x}}$

In the same way, if $A$ denotes angle of right triangle, then

$\tan{A} \,=\, \dfrac{1}{\cot{A}}$

The reciprocal identity of cot function is written in this form but the symbol of angle of right triangle is only changed.