The distance form centre to any point on the circumference of a circle is called radius of the circle.
Every point on the circumference of the circle maintains a constant distance from centre of the circle. The constant distance between them is called as radius. It is popularly denoted by letter $r$ in geometry.
Actually, the distance between two points is same as the length of the line segment which joins two points. Hence, the radius of a circle is geometrically denoted by a line segment which joins centre and any point on the circumference.
$C$ is a centre of a circle and $P$ is any point on the same circle.
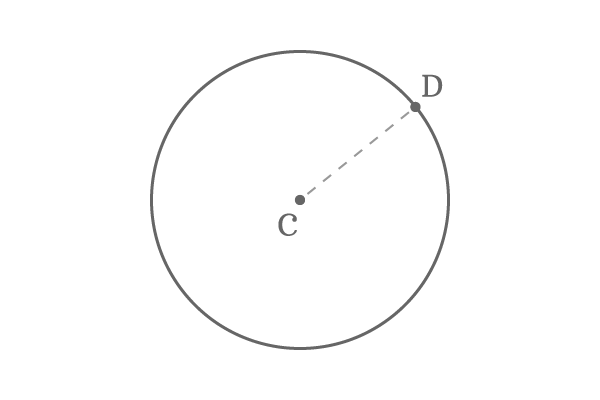
According to definition of radius of a circle, the distance from centre $C$ to any point $P$ on the circumference is known as radius of the circle. If they are joined by a line, then the length of line segment is same as the distance between them.
It means, the radius of a circle is equal to the length of the line segment $\overline{CP}$. Hence, the radius in a circle is denoted by a line segment geometrically.
$\therefore \,\,\,\,\,\, CP \,=\, r$
A best free mathematics education website that helps students, teachers and researchers.
Learn each topic of the mathematics easily with understandable proofs and visual animation graphics.
A math help place with list of solved problems with answers and worksheets on every concept for your practice.
Copyright © 2012 - 2022 Math Doubts, All Rights Reserved