Proof of Product of Limits Rule
The product of limits law is a most important limit formula, which expresses that the limit of product of two or more functions is equal to product of their limits. Now, let’s learn how to prove the limits multiplication rule in calculus mathematically.
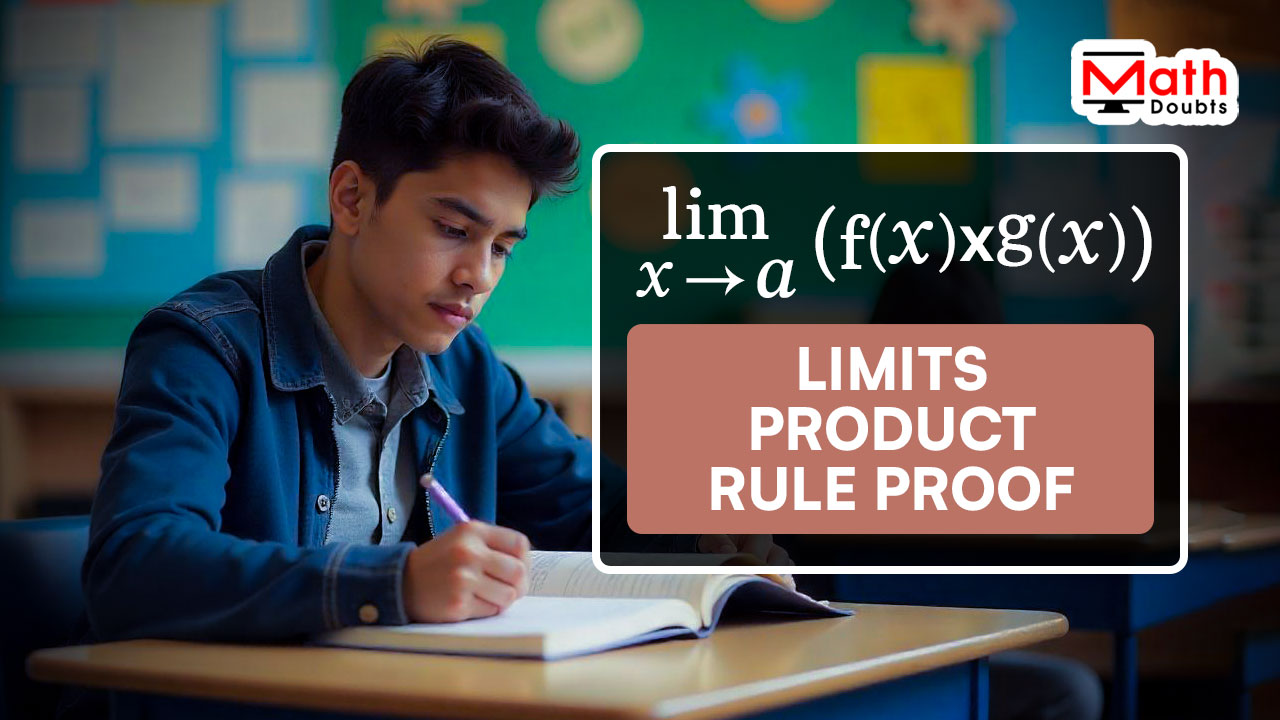
Let’s consider two functions and they both are defined in terms of $x$. Now, the functions are simply written as $f(x)$ and $g(x)$ in mathematics. The multiplication of them is written as $f(x) \times g(x)$ and their product is simply written as $f(x).g(x)$.
Multiplication
The limit of product of functions as its variable $x$ approaches to a value $a$, is written as follows.
$\displaystyle \large \lim_{x \,\to\, a}{\normalsize \big[f(x) \times g(x)\big]}$
Now, let’s begin the procedure of proving the limits product rule by finding the limit of a product.
Step: 1
The limits by direct substitution is a fundamental method in calculus. So, substitute $x$ equals to $a$ in the function to find the limit of the multiplication of functions as the value of $x$ approaches to $a$.
$\implies$ $\displaystyle \large \lim_{x \,\to\, a}{\normalsize \big[f(x) \times g(x)\big]}$ $\,=\,$ $f(a) \times g(a)$
Now, it is time to find the limit of every function by the direct substitution as the value of $x$ tends to $a$.
Step: 2
Substitute $x = a$ in function $f(x)$ to find limit of function $f(x)$ as the value of $x$ is tends to $a$.
$\implies$ $\displaystyle \large \lim_{x \,\to\, a}{\normalsize f(x)}$ $\,=\,$ $f(a)$
The limit of function $f(x)$ as the value of $x$ approaches $a$ is $f(a)$. So, it can be written as follows.
$\,\,\,\,\,\,\therefore\,\,\,$ $f(a)$ $\,=\,$ $\displaystyle \large \lim_{x \,\to\, a}{\normalsize f(x)}$
Similarly, substitute $x = a$ in function $g(x)$ to find the limit of function $g(x)$ as the value of $x$ approaches to value of $a$.
$\implies$ $\displaystyle \large \lim_{x \,\to\, a}{\normalsize g(x)}$ $\,=\,$ $g(a)$
The limit of function $g(x)$ as the value of $x$ approaches $a$ is $g(a)$. So, it can also be written as follows.
$\,\,\,\,\,\,\therefore\,\,\,$ $g(a)$ $\,=\,$ $\displaystyle \large \lim_{x \,\to\, a}{\normalsize g(x)}$
Let’s find the relationship between the functions for proving the product law for limits in calculus.
Step: 3
We have evaluated above that
$\implies$ $\displaystyle \large \lim_{x \,\to\, a}{\normalsize \big[f(x) \times g(x)\big]}$ $\,=\,$ $f(a) \times g(a)$
We have already evaluated above that
$(1).\,\,$ $f(a)$ $\,=\,$ $\displaystyle \large \lim_{x \,\to\, a}{\normalsize f(x)}$
$(2).\,\,$ $g(a)$ $\,=\,$ $\displaystyle \large \lim_{x \,\to\, a}{\normalsize g(x)}$
Now, substitute the values of $f(a)$ and $g(a)$ in the above mathematical equation.
$\,\,\,\,\,\,\therefore\,\,\,$ $\displaystyle \large \lim_{x \,\to\, a}{\normalsize \big[f(x) \times g(x)\big]}$ $\,=\,$ $\displaystyle \large \lim_{x \,\to\, a}{\normalsize f(x)}$ $\times$ $\displaystyle \large \lim_{x \,\to\, a}{\normalsize g(x)}$
It has proved that the limit of product of two functions is equal to the product of their limits. It is called the product rule of limits and it is also called the multiplication rule of limits in calculus.
Extension
The limit product law can also be extended to more than two functions. So, the multiplication rule for limits can be written in the following form and it can also be proved by the above procedure.
Let’s denote functions as $f_{1}{(x)}$, $f_{2}{(x)}$, $f_{3}{(x)} \ldots$, then the product rule of limits is written as follows.
$\displaystyle \large \lim_{x \,\to\, a}{\normalsize \big[f_{1}{(x)} \times f_{2}{(x)} \times f_{3}{(x)}\ldots\big]}$ $\,=\,$ $\displaystyle \large \lim_{x \,\to\, a}{\normalsize f_{1}{(x)}}$ $\times$ $\displaystyle \large \lim_{x \,\to\, a}{\normalsize f_{2}{(x)}}$ $\times$ $\displaystyle \large \lim_{x \,\to\, a}{\normalsize f_{3}{(x)}}$ $\times$ $\ldots$
$\displaystyle \large \lim_{x \,\to\, a} \normalsize \big[f{(x)} \div g{(x)}\big]$
The quotient rule of limits with proof to learn how to find the limit of the quotient of two functions.
