Two or more straight lines which do not intersect each other at any point on the plane are called parallel lines.
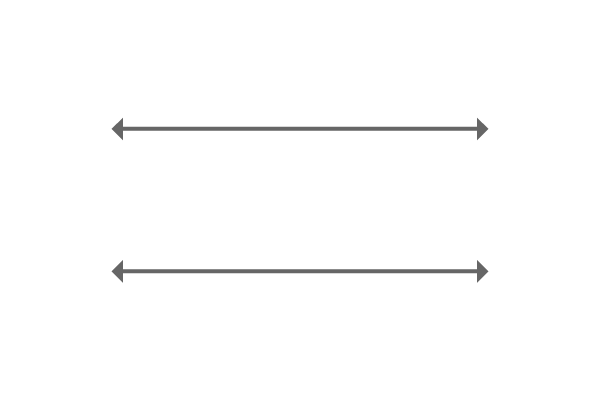
Parallel lines are straight lines basically and they appear on a plane side by side. They never intersect each other anywhere on a plane because of having same angle. Therefore, if two or more straight lines have same angle, then they do not meet each other.
Similarly, the vertical distance between opposite points of them is always same due to the parallelism of the parallel lines.
$\overleftrightarrow{AB}$ and $\overleftrightarrow{CD}$ are two straight lines and they are extended infinitely but they do not intersect each other even though they are appearing side by side.
They maintain equal distance between them at all their opposite points. The reason for this is the angles of both straight lines are same.
The straight lines $\overleftrightarrow{AB}$ and $\overleftrightarrow{CD}$ are called parallel lines.
A double vertical line ($\|$) is used to represent parallelism of the lines mathematically.
The parallel symbol is displayed between straight lines to express that they both are parallel lines.
$\overleftrightarrow{AB} \,\, \| \,\, \overleftrightarrow{CD}$
It is read as $\overleftrightarrow{AB}$ parallel to the $\overleftrightarrow{CD}$.
Similarly, it can also be displayed in other way.
$\overleftrightarrow{CD} \,\, \| \,\, \overleftrightarrow{AB}$
It is read as $\overleftrightarrow{CD}$ parallel to the $\overleftrightarrow{AB}$.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved