Obtuse Triangle

A triangle that contains an obtuse angle is called an obtuse triangle. It is also called as an obtuse angled triangle.

Introduction

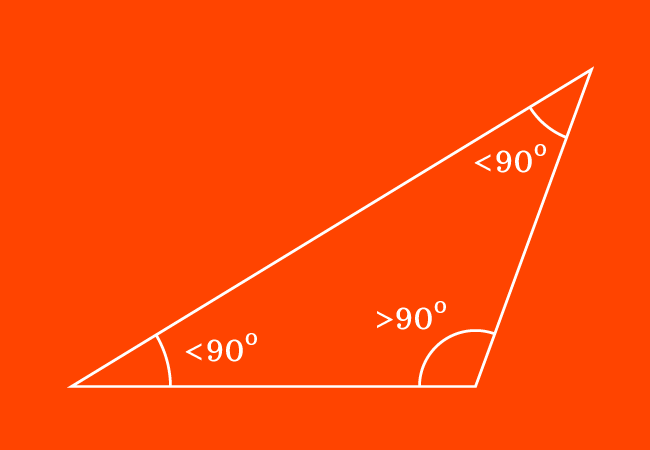
Due to the arrangement of three line segments as a closed geometric shape, three interior angles are formed inside a triangle.

In some cases, one of the three interior angles in a triangle can be an obtuse angle. Hence, the triangle can be called an obtuse triangle. It is also called an obtuse angled triangle.

In an obtuse triangle, one interior angle is an obtuse angle and remaining two interior angles are acute angles.

Construction

Geometrically, an obtuse triangle can be constructed by using geometric tools. So, let’s construct it firstly and then focus on studying its geometric properties practically.

1. Draw a horizontal line segment from point $P$ to $Q$ by a ruler. In this example, the length of the line segment is $7\,cm$.
2. Use protractor and mark a point at an obtuse angle. In this case, it is marked at $105^°$. Now, draw a straight line from point $P$ through the marked point.
3. Take a compass and set it to any length by a ruler. Here, it is set to $6\,cm$. Now, draw an arc on $105^°$ angle line from point $P$ and it is intersected at point $R$.
4. Finally, join the points $Q$ and $R$ by a line for completing the construction of a triangle geometrically.

Thus, a triangle, denoted by $QPR$ is constructed geometrically. In this example, the triangle $QPR$ contains an obtuse angle. Therefore, the triangle $QPR$ is called an obtuse triangle.

Properties

The $\Delta QPR$ contains three interior angles, and they are written as $\angle QPR$, $\angle PQR$ and $\angle QRP$.

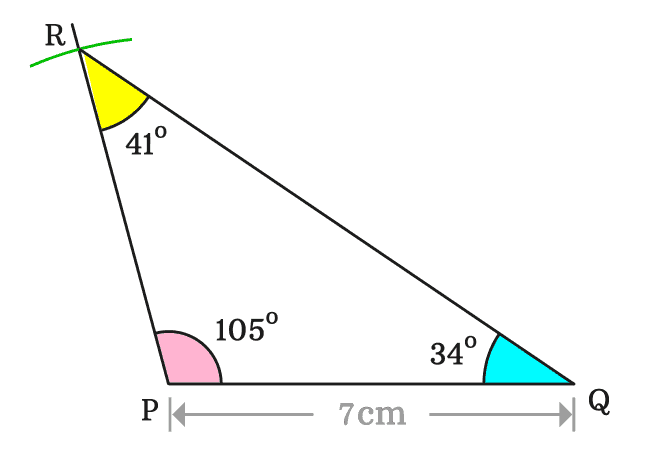
The angle $QPR$ is known and it is $105^°$. Therefore $\angle QPR \,=\, 105^°$

For studying the obtuse angled triangle, we have to measure the remaining angles and it can be done by a protractor.

It is measured that

$(1).\,\,\,$ $\angle PQR \,=\, 34^°$

$(2).\,\,\,$ $\angle QRP \,=\, 41^°$

We can observe that the two angles are acute angles. Therefore, it is cleared that in an obtuse triangle, one angle is an obtuse angle and the remaining two angles are acute angles.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.