Matrix addition
A mathematical operation of adding a matrix to another matrix is called the addition of the matrices.
Introduction
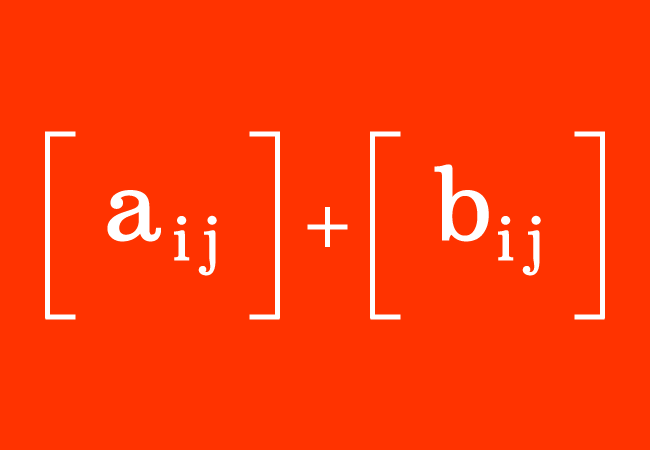
The matrices are involved in addition in some cases in mathematics. Each matrix consists of entries (or elements) in rows and columns. Hence, the matrices cannot be added, same as the addition of the numbers. Hence, a special systemic procedure is required for adding the matrices. Now, let’s learn how to add the matrices in mathematics.
Principle
Each entry of a matrix is added to the corresponding element in the second matrix is the principle for adding the matrices.
Condition
The principle for adding the matrices is applicable if the arrangement of entries in the matrices is the same. It means, the matrices of the same order can be added possibly.
$A$ $\,=\,$ $\begin{bmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n}\\ a_{21} & a_{22} & a_{23} & \cdots & a_{2n}\\ a_{31} & a_{32} & a_{33} & \cdots & a_{3n}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & a_{m3} & \cdots & a_{mn} \end{bmatrix}$ and $B$ $\,=\,$ $\begin{bmatrix} b_{11} & b_{12} & b_{13} & \cdots & b_{1n}\\ b_{21} & b_{22} & b_{23} & \cdots & b_{2n}\\ b_{31} & b_{32} & b_{33} & \cdots & b_{3n}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & b_{m3} & \cdots & b_{mn} \end{bmatrix}$
The $A$ and $B$ are the matrices of the order $m \times n$. The arrangement of the entries in both matrices is the same. Hence. It is possible to add them by adding an entry of one matrix to the corresponding element of the second matrix.
$A+B$ $\,=\,$ $\begin{bmatrix} a_{11}+b_{11} & a_{12}+b_{12} & a_{13}+b_{13} & \cdots & a_{1n}+b_{1n}\\ a_{21}+b_{21} & a_{22}+b_{22} & a_{23}+b_{23} & \cdots & a_{2n}+b_{2n}\\ a_{31}+b_{31} & a_{32}+b_{32} & a_{33}+b_{33} & \cdots & a_{3n}+b_{3n}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{m1}+b_{m1} & a_{m2}+b_{m2} & a_{m3}+b_{m3} & \cdots & a_{mn}+b_{mn} \end{bmatrix}$
The sum of the matrices is also a matrix of the same order.
Remember that it is not possible to add the matrices of the different order because the arrangement of the elements in the matrices are different. Hence, it is not possible to add some entries and the addition is failed in this case.
Examples
Let’s learn how to add the matrices from the following two examples.
$(1).\,\,\,$ $\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix}$ $+$ $\begin{bmatrix} 5 & 6 \\ 7 & 8 \\ \end{bmatrix}$
$\implies$ $\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix}$ $+$ $\begin{bmatrix} 5 & 6 \\ 7 & 8 \\ \end{bmatrix}$ $\,=\,$ $\begin{bmatrix} 1+5 & 2+6 \\ 3+7 & 4+8 \\ \end{bmatrix}$
$\,\,\,\therefore\,\,\,\,\,\,$ $\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix}$ $+$ $\begin{bmatrix} 5 & 6 \\ 7 & 8 \\ \end{bmatrix}$ $\,=\,$ $\begin{bmatrix} 6 & 8 \\ 10 & 12 \\ \end{bmatrix}$
In this way, the square matrices can be added to find the sum of the matrices.
$(2).\,\,\,$ $\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{bmatrix}$ $+$ $\begin{bmatrix} 9 & 7 & 5 \\ 8 & 6 & 4 \\ \end{bmatrix}$
$\implies$ $\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{bmatrix}$ $+$ $\begin{bmatrix} 9 & 7 & 5 \\ 8 & 6 & 4 \\ \end{bmatrix}$ $\,=\,$ $\begin{bmatrix} 1+9 & 2+7 & 3+5 \\ 4+8 & 5+6 & 6+4 \\ \end{bmatrix}$
$\,\,\,\therefore\,\,\,\,\,\,$ $\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{bmatrix}$ $+$ $\begin{bmatrix} 9 & 7 & 5 \\ 8 & 6 & 4 \\ \end{bmatrix}$ $\,=\,$ $\begin{bmatrix} 10 & 9 & 8 \\ 12 & 11 & 10 \\ \end{bmatrix}$
Thus, the rectangular matrices can be added for evaluating the sum of the matrices.
Problems
List of the questions on matrix addition with solutions for practice to learn how to add the matrices of the same order in mathematics.
