Point slope form of a Line

Equation

$y-y_{1} \,=\, m(x-x_{1})$

It is an equation of a straight line when a straight line intercepts $x$-axis at a point with some slope.

Proof

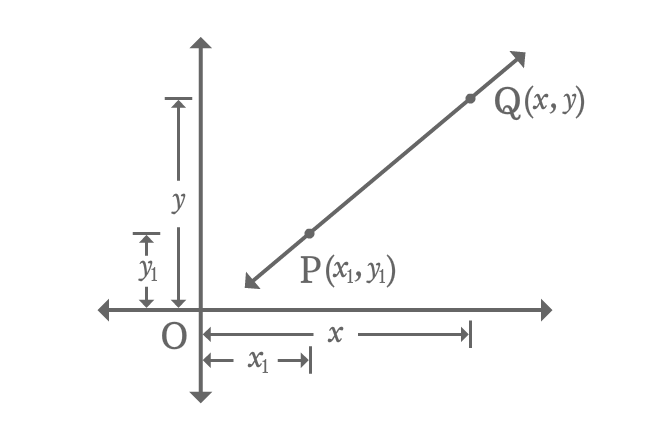
$P(x_{1}, y_{1})$ is a point on straight line and $Q(x, y)$ is any point on the same straight line. The straight line $\small \overleftrightarrow{PQ}$ has some slope in Cartesian coordinate system.

The slope of the line is denoted by $m$ in geometric system.

Draw a parallel line to horizontal axis from point $P$ and also draw a perpendicular line towards $x$-axis from point $Q$. The two lines are intersected at point $R$. Thus, a right triangle $\Delta RPQ$ is formed geometrically.

The angle of the $\Delta RPQ$ is theta ($\theta$) and then calculate the slope of the straight line.

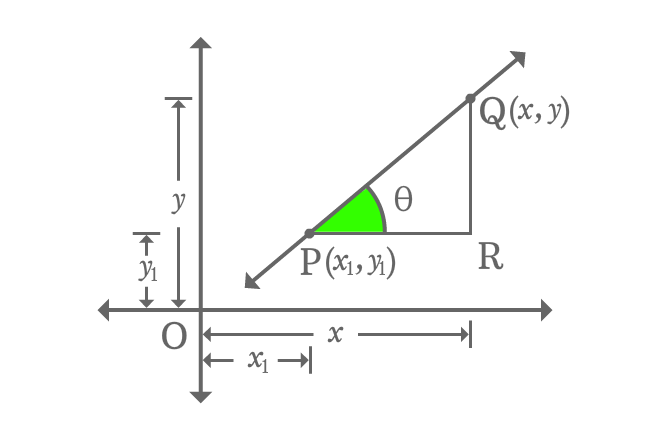
$m \,=\, \tan{\theta}$

Evaluate tan of angle theta to express slope of the line in terms of coordinates of the line.

$\implies m \,=\, \dfrac{QR}{PR}$

$\implies m \,=\, \dfrac{OQ-OR}{OR-OP}$

$\implies m \,=\, \dfrac{y-y_{1}}{x-x_{1}}$

$\implies m(x-x_{1}) \,=\, y-y_{1}$

$\,\,\, \therefore \,\,\,\,\,\, y-y_{1} \,=\, m(x-x_{1})$

It is a linear equation and it is in terms of a point and slope. So, the equation of straight line is called as point-slope form equation of a straight line.