Product Rule of the Exponents having same Base

Formula

$b^{\displaystyle m} \times b^{\displaystyle n} \,=\, b^{\displaystyle m {\small \,+\,} n}$

The product of multiplication of exponents with the same base is equal to the sum of their powers with same base, is called the product rule of exponents with same base.

Introduction

In mathematics, two or more exponents with the same base are involved in multiplication in some cases. Like multiplying the numbers, the exponents having the same base cannot be multiplied directly due to the quantities in exponential notation. So, it requires a special multiplication rule to find their product and it is called the product rule of the exponents having the same base.

Let’s learn what the product rule of exponents is, when the exponents have same base.

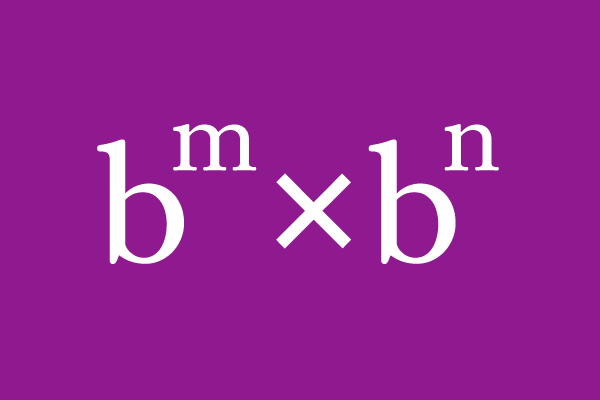
Consider two quantities and denote them by $p$ and $q$. Now, split each quantity as the product of factors based on another quantity $b$.

$(1).\,\,$ $p$ $\,=\,$ $\underbrace{b \times b \times b \times b \times \cdots \times b}_{\displaystyle m \, factors}$ $\,=\,$ $b^{\displaystyle m}$

Let’s consider that the total number of factors in $b$ is $m$. So, the quantity $p$ can be written as the $b$ raised to the power of $m$.

$(2).\,\,$ $q$ $\,=\,$ $\underbrace{b \times b \times b \times \cdots \times b}_{\displaystyle n \, factors}$ $\,=\,$ $b^{\displaystyle n}$

Similarly, let’s assume that the total number of factors in $b$ is $n$. So, the quantity $q$ can be written as the $b$ raised to the power of $n$.

Now, multiply the quantities in exponential form to find their product.

$\implies$ $b^{\displaystyle m} \times b^{\displaystyle n}$

Property

$(1).\,\,$ $2^3 \times 2^4$ $\,=\,$ $2^{3{\large +}4}$

$(2).\,\,$ $3^2 \times 3^5$ $\,=\,$ $3^{2{\large +}5}$

Learn how the product of exponents having the same is equal to the sum of the exponents with the same base, from some simple arithmetic expressions.

The product of exponents having the same base is equal to the sum of the exponents with same.

$\,\,\,\therefore\,\,\,\,\,\,$ $b^{\displaystyle m} \times b^{\displaystyle n} \,=\, b^{\displaystyle m {\small \,+\,} n}$

Extension

The product rule of exponents having the same base is not limited to two factors and it can be extended to more than two factors in exponential form.

$b^{\displaystyle m}$ $\times$ $b^{\displaystyle n}$ $\times$ $b^{\displaystyle o}$ $\times$ $\cdots$ $\,=\,$ $b^{\displaystyle m+n+o+ \cdots}$

Use

The product law of powers with same base is used in two different cases.

1. The product of exponents with same base is simplified as the sum of the exponents with the same base.
2. The addition of exponents with a base is expanded as the product of the exponents with the same base.

Proof

Learn how to prove the product rule of indices with same base in mathematics.

Verification

The product of two numbers $16$ and $64$ is $1024$.

$16 \times 64 \,\,=\,\, 1024$

Express, $16$, $64$ and $1024$ in exponential notation on the basis of number $4$.

$(1)\,\,\,\,\,\,$ $16 = 4 \times 4 = 4^2$

$(2)\,\,\,\,\,\,$ $64 = 4 \times 4 \times 4 = 4^3$

$(3)\,\,\,\,\,\,$ $1024 = 4 \times 4 \times 4 \times 4 \times 4 = 4^5$

Now, write the mathematical relationship between $16$, $64$ and $1024$ in the form of exponents with same base.

$16 \times 64 \,\,=\,\, 1024$

$\implies 4^2 \times 4^3 \,\,=\,\, 4^5$

Observe the exponents of the three exponential terms, it clears that the product of exponents with the same base can be obtained by adding the exponents with the same base.

$\therefore \,\,\,\,\,\, 4^2 \times 4^3 \,\,=\,\, 4^{2\,+\,3}$

Worksheet

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.