Fourth Quadrant

The right-bottom side region in the two dimensional space is called the fourth quadrant.

Introduction

Two number lines get bisected perpendicularly at their middle point in two-dimensional Cartesian coordinate system to split the coordinate plane into four equal regions.

The right-bottom side region is called the fourth quadrant. In this case, the region in the angle $XOY’$ is the fourth quadrant and represented by a Roman numeral $IV$.

In $\angle XOY’$, the $x$-axis represents positive values and $y$-axis represents negative values. The signs of both abscissa and ordinate of each point in this region should be positive and negative respectively.

If $x$-coordinate and $y$-coordinate of every point are denoted by $x$ and $y$ respectively, then the values of them are written mathematically as $x > 0$ and $y < 0$.

Usage

In two dimensional space, the fourth quadrant is used to identity the location of a point whose abscissa is positive and ordinate is negative. Let’s begin it to learn how to use the fourth quadrant in the coordinate geometry.

Example

Identify the location of the point $D(5, -3)$.

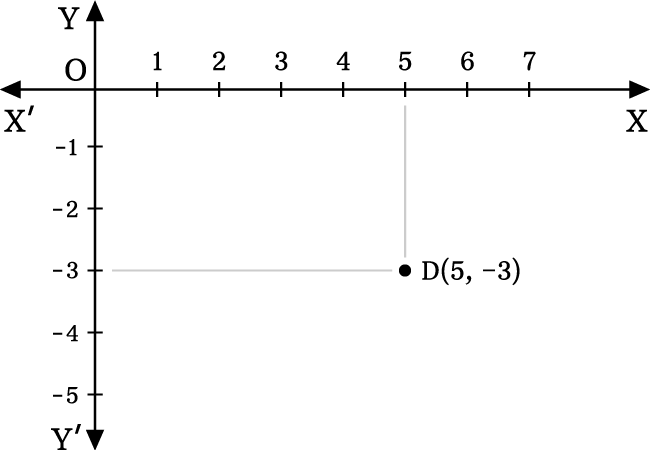
The $x$ coordinate (or abscissa) is $5$ and $y$ coordinate (or ordinate) is $-3$ in this example.

Identity $5$ on positive $x$-axis. Draw a line from $5$ but it should be parallel to negative $y$ axis and perpendicular to positive $x$ axis.
Identify $-3$ on negative $y$ axis. Draw a line from $-3$ but it should be perpendicular to negative $y$ axis and parallel to positive $x$ axis.
The two lines get intersected perpendicularly at a point in the plane and it is the point $D(5, -3)$.

In this way, the fourth quadrant of bi dimensional Cartesian coordinate system is used for identifying the location of any point whose abscissa is positive and ordinate is negative.