Factorization (or Factorisation) by Splitting the Middle term

Method

A method of factoring a quadratic polynomial as a product of two linear expressions by splitting the term is called the factorization by splitting the middle term.

Introduction

A quadratic polynomial is a second degree polynomial, which is written in general form as follows.

$ax^2+bx+c$

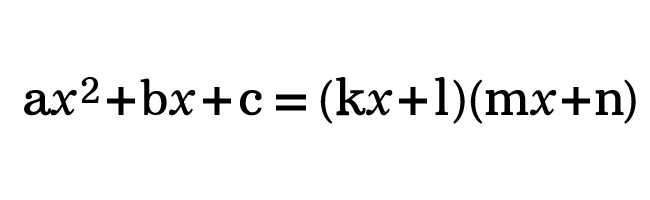
It should be factored in some cases in mathematics. So, it is essential for everyone to learn how to factorize a polynomial in quadratic form.

We know that the product of two linear expressions in one variable forms a quadratic expression. So, a quadratic expression can be written as a product of two linear expressions.

$\implies$ $ax^2+bx+c$ $\,=\,$ $(kx+l)(mx+n)$

The factorizing the quadratic expression is possible when the middle term is split as two terms in the expression, and the process is called in the following three ways in mathematics.

1. Factorization by splitting the middle term.
2. Factorisation by splitting the middle term.
3. Factoring by splitting the middle term.

Now, it is time to clearly learn what the middle term splitting method is.

Knowledge

The knowledge on factoring by grouping is required to understand the middle term splitting factorization.

Procedure

There are four simple steps to factorize a quadratic expression by splitting the middle term.

1. Make sure that all the terms in a quadratic expression are written in descending order.
2. Find the product of first and last terms by considering their signs.
3. Split the middle as either the sum or difference of two terms but their product should be equal to the product of first and last terms.
4. Finally, factorize the expression by the grouping method.

Now, let us learn how to split the middle term for factorising the quadratic expression.

Example

Factorise $6x+x^2+8$

Write the expression in an order

Firstly, let us check whether the terms in the expression are written in descending order. In this example question, the terms are written not in descending order. So, write the terms in the quadratic polynomial in descending order.

$\implies$ $x^2+6x+8$

Find the Product of the two terms

Now, consider the first and last terms with their signs and find their product by the multiplication.

$\implies$ $x^2 \times 8$ $\,=\,$ $8x^2$

Check the condition to split the middle term

Now, consider the middle term $6x$ and try to split it as either sum or difference of two terms, but their product should be equal to the product of first and last terms.

$(1).\,\,$ $2x+4x \,=\, 6x$

$(2).\,\,$ $2x \times 4x \,=\, 8x^2$

Therefore, let us write the expression by splitting the middle term of the quadratic polynomial.

$\implies$ $x^2+2x+4x+8$

Factorize the expression by grouping

Finally, consider two terms as a group based on a common factor. Now, the four terms expression is considered as two groups.

$= \,\,\,$ $(x^2+2x)+(4x+8)$

Now, take the common factor our from each group to finish the process of factoring a quadratic polynomial by using the splitting the middle term factorisation method.

$= \,\,\,$ $x(x+2)+4(x+2)$

$= \,\,\,$ $(x+2)(x+4)$

Therefore, the given trinomial $x^2+6x+8$ is factored as $(x+2)(x+4)$ by splitting the middle of the given expression.

Worksheet

The list of questions with solutions to learn how to factorise an expression by splitting the middle term.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.