The quotient of one plus sine of angle $x$ divided by cosine of angle $x$ plus cosine of angle $x$ divided by one plus sine of angle $x$ should be evaluated in this trigonometry problem.
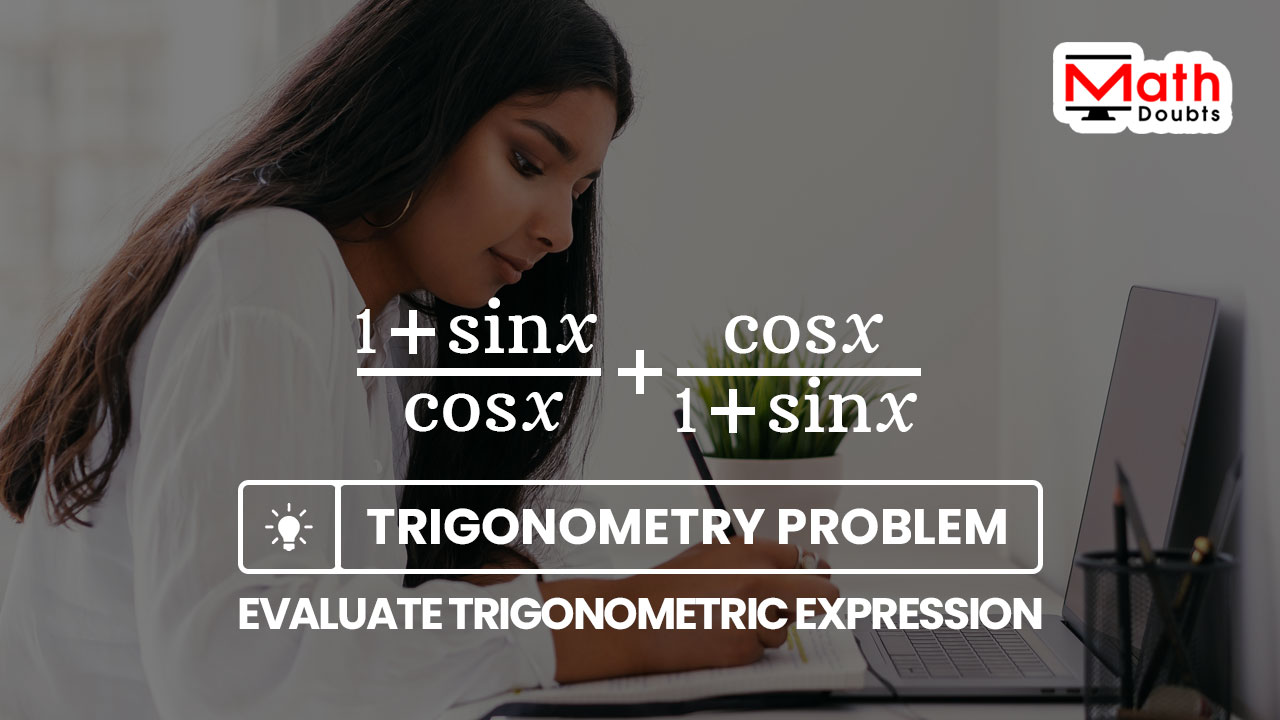
The one plus sine of angle $x$ divided by cosine of angle $x$ is a fraction and the cosine of angle $x$ divided by one plus sine of angle $x$ is another fraction, and they both are connected by a plus sign to form a trigonometric expression.
$\dfrac{1+\sin{x}}{\cos{x}}$ $+$ $\dfrac{\cos{x}}{1+\sin{x}}$
Look at the denominators of the both rational functions in the trigonometric expression. The denominators of the both fractions in the given trigonometric expression are different and it is not possible to add them directly. So, let’s convert the unlike trigonometric fractions as the like trigonometric fractions.
The first term should have $1$ plus sine of angle $x$ in the denominator. Similarly, the second term should have cosine of angle $x$ in the denominator. Then only, the two unlike fractions become the like trigonometric fractions.
$=\,\,\,$ $1 \times \dfrac{1+\sin{x}}{\cos{x}}$ $+$ $1 \times \dfrac{\cos{x}}{1+\sin{x}}$
$=\,\,\,$ $\dfrac{1+\sin{x}}{1+\sin{x}}$ $\times$ $\dfrac{1+\sin{x}}{\cos{x}}$ $+$ $\dfrac{\cos{x}}{\cos{x}}$ $\times$ $\dfrac{\cos{x}}{1+\sin{x}}$
Now, multiply the fractions in each term of the trigonometric expression.
$=\,\,\,$ $\dfrac{(1+\sin{x}) \times (1+\sin{x})}{(1+\sin{x}) \times \cos{x}}$ $+$ $\dfrac{\cos{x} \times \cos{x}}{\cos{x} \times (1+\sin{x})}$
The factors in the numerator of each term in the trigonometric expression are same. So, the product of them can be expressed in exponential notation.
$=\,\,\,$ $\dfrac{(1+\sin{x})^2}{(1+\sin{x}) \times \cos{x}}$ $+$ $\dfrac{\cos^2{x}}{\cos{x} \times (1+\sin{x})}$
The places of the factors in the denominator of first term can be switched in the trigonometric expression by using the commutative property of the multiplication.
$=\,\,\,$ $\dfrac{(1+\sin{x})^2}{\cos{x} \times (1+\sin{x})}$ $+$ $\dfrac{\cos^2{x}}{\cos{x} \times (1+\sin{x})}$
The denominators of the two fractions in the trigonometric expression are same, which means they are like trigonometric fractions. Now, the fractions having the same denominators can be added by the addition of the like fractions to find the sum of them.
$=\,\,\,$ $\dfrac{(1+\sin{x})^2+\cos^2{x}}{\cos{x} \times (1+\sin{x})}$
In the numerator, two terms in square form are added but the first term is a square of a binomial. So, it can be expanded by the square of sum of two terms formula.
$=\,\,\,$ $\dfrac{1^2+(\sin{x})^2+2 \times 1 \times \sin{x}+\cos^2{x}}{\cos{x} \times (1+\sin{x})}$
Now, find the values of square of one, square of sine of angle $x$ and the product of two, one and sine of angle $x$ in the numerator.
$=\,\,\,$ $\dfrac{1 \times 1+\sin{x} \times \sin{x}+2\sin{x}+\cos^2{x}}{\cos{x} \times (1+\sin{x})}$
$=\,\,\,$ $\dfrac{1+\sin^2{x}+2\sin{x}+\cos^2{x}}{\cos{x} \times (1+\sin{x})}$
The places of the terms in the numerator can be changed as per the commutative property of the addition.
$=\,\,\,$ $\dfrac{1+\sin^2{x}+\cos^2{x}+2\sin{x}}{\cos{x} \times (1+\sin{x})}$
According to the pythagorean identity of sine and cosine functions, the sum of squares of sine and cosine of angle $x$ is equal to one.
$=\,\,\,$ $\dfrac{1+1+2\sin{x}}{\cos{x} \times (1+\sin{x})}$
$=\,\,\,$ $\dfrac{2+2\sin{x}}{\cos{x} \times (1+\sin{x})}$
The number two is a common factor in the both terms of the numerator and it can be taken out common from them.
$=\,\,\,$ $\dfrac{2 \times 1+2 \times \sin{x}}{\cos{x} \times (1+\sin{x})}$
The trigonometric expression can be factored by taking out the common factor $2$ from the terms in the numerator.
$=\,\,\,$ $\dfrac{2 \times (1+\sin{x})}{\cos{x} \times (1+\sin{x})}$
The one place sine of angle $x$ is a common factor in both numerator and denominator. So, they both get cancelled each other in the rational function.
$=\,\,\,$ $\dfrac{2 \times \cancel{(1+\sin{x})}}{\cos{x} \times \cancel{(1+\sin{x})}}$
$=\,\,\,$ $\dfrac{2}{\cos{x}}$
The trigonometric function cosine of angle $x$ is in denominator and it can be separated from the fraction for expressing the reciprocal of cosine function in its simplified form.
$=\,\,\,$ $\dfrac{2 \times 1}{\cos{x}}$
According to the multiplication of the fractions, the fraction can be split as a product of two fractions for our convenience.
$=\,\,\,$ $2 \times \dfrac{1}{\cos{x}}$
Now, the reciprocal of cosine trigonometric identity can be used to simplify the reciprocal of cosine of angle $x$ as the secant of angle $x$.
$=\,\,\,$ $2 \times \sec{x}$
$=\,\,\,$ $2\sec{x}$
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved