Proof of Equation of a circle centered at the origin

The circle centered at the origin of the two dimensional space is written in following mathematical form.

$x^2+y^2$ $\,=\,$ $r^2$

Let us learn how to derive the equation of a circle in standard mathematical form when the center (or centre) of a circle is exactly located at the origin of the bi-dimensional space.

Construction of a Triangle inside a Circle

A right triangle (or right angled triangle) should be constructed for deriving a standard equation of a circle when the circle is centered at the origin of the two dimensional cartesian coordinate system.

A right angled triangle inside a circle whose center (or centre) is exactly located at origin in the two dimensional cartesian coordinate system can be constructed as per the following steps.

1. Let’s denote the origin of the two-dimensional cartesian coordinate system by $O$ and draw a circle, which is centered at the origin. It means, the center (or centre) of circle $C$ is exactly located at the origin of the two dimensional space.
2. Consider a point on the circumference of circle and it is denoted by $P$. Let us assume that the point $P$ is $x$ and $y$ units away from the origin in both horizontal and vertical directions. Therefore, the point $P$ in coordinate form is written as $P(x, y)$.
3. Connect the point $P$ and the centre (or center) or origin by a straight line and it represents the radius of the circle geometrically. Let’s assume that the radius of the circle is $r$ units.
4. Draw a perpendicular line to $x$-axis from point $P$ and it intersects the horizontal axis at point $Q$. Thus, it forms a right angled triangle, which is written as $\Delta QOP$ or $\Delta QCP$.

Calculate the lengths of sides of Triangle

In $\Delta QCP$ or $\Delta QOP$, the opposite side is $\overline{PQ}$, the adjacent side is $\overline{OQ}$ or $\overline{CQ}$ and the hypotenuse is $\overline{OP}$ or $\overline{CP}$. Their lengths are written in mathematical form as $PQ, OQ$ or $CQ$ and $OP$ or $CP$ respectively.

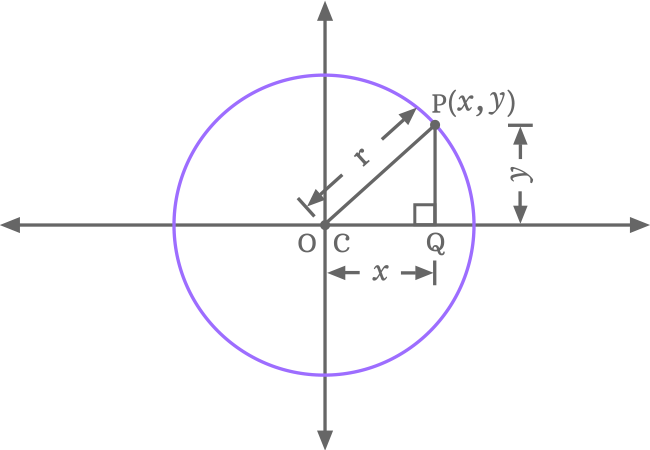
It is time to calculate the length of each side of the right angled triangle.

1. $OQ$ $\,=\,$ $CQ$ $\,=\,$ $x$
2. $PQ$ $\,=\,$ $y$
3. $OP$ $\,=\,$ $CP$ $\,=\,$ $r$

Write the relation between the sides

According to the Pythagorean Theorem, the lengths of all three sides of right angled triangle $POQ$ or $PCQ$ can be written as a mathematical relation.

${CP}^2$ $\,=\,$ ${CQ}^2+{PQ}^2$

$\implies$ ${OP}^2$ $\,=\,$ ${OQ}^2+{PQ}^2$

We know that the $CQ$ or $OQ$ is length of opposite side, $PQ$ is length of adjacent side and $OP$ or $CP$ is length of hypotenuse. Now, substitute the lengths of them in the above mathematical equation.

$\implies$ $r^2$ $\,=\,$ $x^2+y^2$

$\,\,\,\therefore\,\,\,\,\,\,$ $x^2+y^2$ $\,=\,$ $r^2$

It is a standard mathematical equation of a circle when the circle is centered at the origin of two dimensional cartesian coordinate system.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.