Diameter

The straight distance between two points on a circle through its center is called the diameter.

Introduction

The diameter is the distance between any two opposite points on a circle but the opposite points are defined by considering the center (or centre) of a circle.

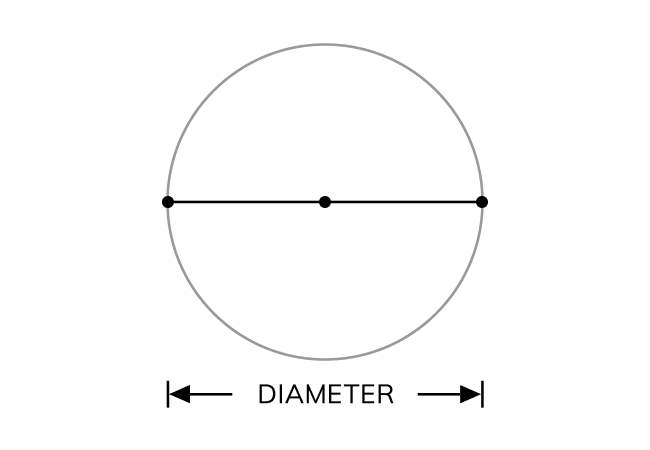
Hence, the diameter of a circle is measured from any point on a circle to its opposite point on the same circle through the centre (or center) of circle.

Representation

It is expressed graphically by a line segment between two opposite points through the center of a circle. It is usually denoted by an alphabet $d$ in geometric mathematics.

Property

In a circle, the diameter is equal to two times the radius.

$Diameter \, (d)$ $\,=\,$ $2 \times Radius$

This geometrical relationship is used as a formula in geometry to find diameter from radius and vice versa.

Example

Let $E$ be any point on the circle and $F$ be its reflection in the point of view of its center or centre ($C$).

Now, draw a straight line from point $E$ to $F$ through $C$. It forms a line segment $\overline{EF}$ and the length of that line segment is called the diameter.

$\implies$ $Diameter \,(d) \,=\, EF$

$\implies$ $Diameter \,(d) \,=\, EC+CF$

In this case, the distance between points $C$ and $E$ and also distance between points $C$ and $F$ is the radius of this circle.

$\,\,\,\therefore\,\,\,\,\,\,$ $d \,= \, 2 \times CF$ (or) $d \,= \, 2 \times CE$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.