Proof of Pythagorean identity of Cosecant and Cotangent functions

Actually, the Pythagorean identity of cosecant and cot functions is proved mathematically in trigonometry by the geometrical method. So, let us study how to derive the proof of the Pythagorean identity for the co-secant and co-tangent functions.

Write the relation between sides of the triangle

Draw a right triangle, assumed as $\Delta CAB$ and its angle is represented by theta.

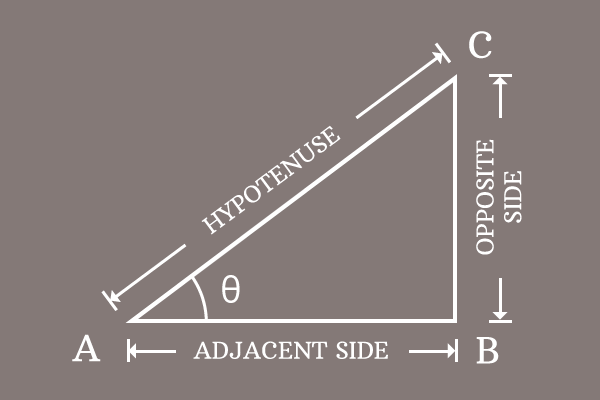
The lengths of opposite side ($\overline{BC}$), adjacent side ($\overline{AB}$) and hypotenuse ($\overline{AC}$) are written as $BC$, $AB$ and $AC$ mathematically. The relationship between them can be written in mathematical form by the Pythagorean theorem.

${AC}^2 = {AB}^2+{BC}^2$

It is an equation that represents the Pythagorean theorem and this equation will be used in deriving the Pythagorean identity of cosecant and cot functions.

Express the sides in trigonometric functions

As per the right triangle $CAB$, write the lengths of the sides in terms of the co-secant and cotangent functions. For doing it, we have to write the cosecant and cot functions in their ratio form firstly.

$\csc{\theta} \,=\, \dfrac{AC}{BC}$

$\implies$ $AC = BC \times \csc{\theta}$

$\cot{\theta} \,=\, \dfrac{AB}{BC}$

$\implies$ $AB = BC \times \cot{\theta}$

Express the equation in trigonometric form

In previous step, We have derived the lengths of the adjacent side and hypotenuse in trigonometric functions.

$AC = BC \times \csc{\theta}$
$AB = BC \times \cot{\theta}$

Now, replace them in the equation, which represents the relation between the sides of the right triangle.

${AC}^2 = {AB}^2+{BC}^2$

$\implies$ $(BC \times \csc{\theta})^2 = (BC \times \cot{\theta})^2+{BC}^2$

The square of a product can be simplified by the power of a product rule.

$\implies$ $(BC)^2 \times (\csc{\theta})^2$ $\,=\,$ $(BC)^2 \times (\cot{\theta})^2+{BC}^2$

$\implies$ ${BC}^2 \times \csc^2{\theta}$ $\,=\,$ ${BC}^2 \times \cot^2{\theta}+{BC}^2$

$\implies$ ${BC}^2 \times \csc^2{\theta}$ $\,=\,$ ${BC}^2 \times \cot^2{\theta}+{BC}^2 \times 1$

$BC^2$ is a common factor in the expression of the right hand side of the equation and they can be taken out common from the terms by the factorization.

$\implies$ ${BC}^2 \times \csc^2{\theta}$ $\,=\,$ ${BC}^2 \times (\cot^2{\theta}+1)$

$\implies$ ${BC}^2 \times \csc^2{\theta}$ $\,=\,$ ${BC}^2 \times (1+\cot^2{\theta})$

$\implies$ $\csc^2{\theta}$ $\,=\,$ $\dfrac{{BC}^2 \times (1+\cot^2{\theta})}{{BC}^2}$

$\implies$ $\csc^2{\theta}$ $\,=\,$ $\require{cancel} \dfrac{\cancel{{BC}^2} \times (1+\cot^2{\theta})}{\cancel{{BC}^2}}$

$\implies$ $\csc^2{\theta}$ $\,=\,$ $1+\cot^2{\theta}$

$\,\,\, \therefore \,\,\,\,\,\,$ $\csc^2{\theta}-\cot^2{\theta} \,=\, 1$

Therefore, it is derived that the subtraction of square of cot of an angle from the cosecant squared of angle is equal to one. It is called as the Pythagorean identity of cosecant and cotangent functions.