Proof of Cot double angle formula

$\cot{2x}$, $\cot{2\theta}$, $\cot{2A}$, $\cot{2\alpha}$ and etc. are examples for cot of double angle function. They can be expanded as given below in terms of cot of angle.

$(1) \,\,\,\,\,\,$ $\cot{2\theta} \,=\, \dfrac{\cot^2{\theta}-1}{2\cot{\theta}}$

$(2) \,\,\,\,\,\,$ $\cot{2x} \,=\, \dfrac{\cot^2{x}-1}{2\cot{x}}$

$(3) \,\,\,\,\,\,$ $\cot{2A} \,=\, \dfrac{\cot^2{A}-1}{2\cot{A}}$

$(4) \,\,\,\,\,\,$ $\cot{2\alpha} \,=\, \dfrac{\cot^2{\alpha}-1}{2\cot{\alpha}}$

Let us prove cot double angle identity in trigonometric mathematics before using it as a formula.

Proof

Cot double angle identity is actually derived in trigonometry by geometric mathematics as per the mathematical relations between angles and sides.

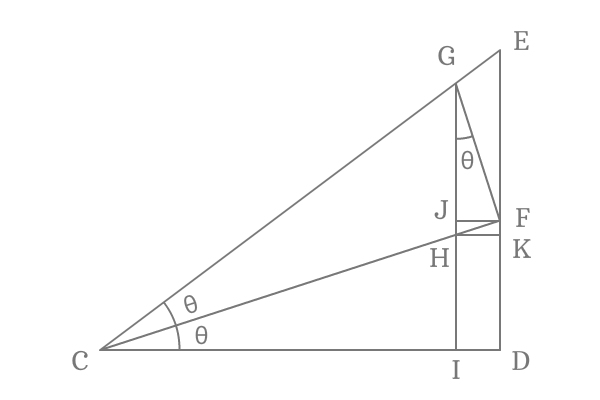
Construction of a Triangle with double angle

$\Delta DCE$ is a right angled triangle. Draw a line from point $C$ to side $\overline{DE}$ to bisect the angle and each angle is $\theta$.

animation for constructing double angle triangle

Draw a perpendicular line to side $\overline{CE}$ from point $F$ and intersects the side $\overline{CE}$ at point $G$. After that, draw a perpendicular line to side $\overline{CD}$ from point $G$. It intersects the side $\overline{CF}$ at point $H$ and also intersects the side $\overline{CD}$ at point $I$.

Draw perpendicular lines to sides $\overline{DE}$ and $\overline{GI}$ from points $H$ and $F$ respectively and their associated intersecting points are $K$ and $J$.

Expressing Cotangent double angle in terms of ratio of sides

Firstly, express cotangent of double angle in terms of ratio of the sides and $2\theta$ is double angle of $\Delta GCI$. So, consider this triangle and write cot of double angle ($\cot{2\theta}$) in terms of ratio of sides of this triangle.

$\cot{2\theta} \,=\, \dfrac{CI}{GI}$

The length of the side $\overline{CI}$ can be written as the subtraction of the lengths of side $\overline{ID}$ from $\overline{CD}$. Similarly, the length of the side $\overline{GI}$ can be written as the sum of the lengths of the sides $\overline{GJ}$ and $\overline{JI}$.

Therefore, $CI = CD -ID$ and $GI = GJ+JI$

$\implies$ $\cot{2\theta} \,=\, \dfrac{CD -ID}{GJ+JI}$

Converting the equation in terms of cot of angle

$\overline{CD}$ is adjacent side of the $\Delta FCD$ and the length of the side $\overline{CD}$ can be written in terms of cot of angle as per this triangle.

$\cot{\theta} \,=\, \dfrac{CD}{DF}$

$\implies$ $CD \,=\, DF \times \cot{\theta}$

$\,\,\, \therefore \,\,\,\,\,\, $ $\cot{2\theta} \,=\, \dfrac{DF \times \cot{\theta} -ID}{GJ+JI}$

$\overline{GI}$ and $\overline{DE}$ are parallel lines. So, the length of the side $\overline{JI}$ is equal to the length of the side $\overline{DF}$. In other words, $DF = JI$. Therefore, replace the length of the side $\overline{JI}$ by $\overline{DF}$.

$\implies$ $\cot{2\theta} \,=\, \dfrac{DF \times \cot{\theta} -ID}{GJ+DF}$

Similarly, $\overline{ID}$ and $\overline{JF}$ both are parallel lines and their lengths are also equal geometrically. Therefore $ID = JF$. Now, replace the length of the side $\overline{ID}$ by the length of the side $\overline{JF}$.

$\implies$ $\cot{2\theta} \,=\, \dfrac{DF \times \cot{\theta} -JF}{GJ+DF}$

The proof of expansion of cot double angle cannot be derived further unless we understand the properties of some sides.

Evaluating angle of the internal triangle

$\Delta FCD$ and $\Delta FHK$ both are similar triangles. Due to this reason, $\angle FHK$ is exactly equal to the $\angle FCD$. Therefore, $\angle FHK = \angle FCD = \theta$.

$\overline{HF}$ is a transversal to the parallel lines $\overline{FJ}$ and $\overline{KH}$. It causes, $\angle FHK$ and $\angle HFJ$ are interior alternative angles. Hence, the $\angle HFJ$ is equal to the $\angle FHK$. Therefore, $\angle HFJ = \angle FHK = \theta$.

The $\angle GFJ$ can be calculated by subtracting the $\angle HFJ$ from $\angle HFG$.

$\angle GFJ = \angle HFG -\angle HFJ$

According to our procedure, the $\angle HFG$ is right angle ($90^\circ$) and already know that $\angle HFJ$ is $\theta$.

$\,\,\, \therefore \,\,\,\,\,\, \angle GFJ = 90^\circ -\theta$

The geometrical investigation revealed the $\angle GFJ$ and the $\angle FJG$ is a right angle as per our step by step geometrical construction of this triangle. The $\angle JGF$ can be determined by this geometrical data.

Apply sum of angles of a triangle rule to $\angle JGF$ to find $\angle JGF$.

$\angle JGF + \angle GFJ + \angle FJG = 180^\circ$

$\implies$ $\angle JGF + 90^\circ -\theta + 90^\circ = 180^\circ$

$\implies$ $\angle JGF + 180^\circ -\theta = 180^\circ$

$\implies$ $\angle JGF = 180^\circ -180^\circ +\theta$

$\,\,\ \therefore \,\,\,\,\,\, \angle JGF = \theta$

Continuing the derivation of cot of double angle

Recollect the expansion of cot double angle.

$\cot{2\theta} \,=\, \dfrac{DF \times \cot{\theta} -JF}{GJ+DF}$

$\overline{GJ}$ is adjacent side of the $\Delta JGF$. It can be used to express length of the side $\overline{GJ}$ in terms of cot of angle.

$\cot{\theta} \,=\, \dfrac{GJ}{JF}$

$\implies$ $GJ \,=\, JF \times \cot{\theta}$

Substitute the length of side $\overline{GJ}$ in the expansion of the cot of double angle equation.

$\implies$ $\cot{2\theta} \,=\, \dfrac{DF \times \cot{\theta} -JF}{JF \times \cot{\theta} +DF}$

Take $JF$ common from both numerator and denominator of the equation for simplifying it further.

$\implies$ $\cot{2\theta} \,=\, \dfrac{JF \Bigg(\dfrac{DF}{JF} \times \cot{\theta} -1\Bigg)}{JF \Bigg(\cot{\theta} +\dfrac{DF}{JF}\Bigg)}$

$\implies$ $\cot{2\theta} \,=\, \require{cancel} \dfrac{\cancel{JF} \Bigg(\dfrac{DF}{JF} \times \cot{\theta} -1\Bigg)}{\cancel{JF} \Bigg(\cot{\theta} +\dfrac{DF}{JF}\Bigg)}$

$\implies$ $\cot{2\theta} \,=\, \dfrac{\dfrac{DF}{JF} \times \cot{\theta} -1}{\cot{\theta} +\dfrac{DF}{JF}}$