Proof for Cosine by Sine Quotient identity

According to the quotient of cosine by sine identity, the quotient of cosine by sine is equal to the cotangent.

$\dfrac{\cos{\theta}}{\sin{\theta}} \,=\, \cot{\theta}$

The trigonometric quotient identity is derived geometrically in mathematical form from a right triangle. Now, it’s your time to learn how to prove the quotient of cosine by sine identity from a geometric shape right triangle.

$\Delta BAC$ is a right angled triangle. In this triangle, $\overline{BC}$, $\overline{AB}$ and $\overline{AC}$ are opposite side, adjacent side and hypotenuse respectively, and the angle of this triangle is taken as theta.

Define Cosine and Sine functions

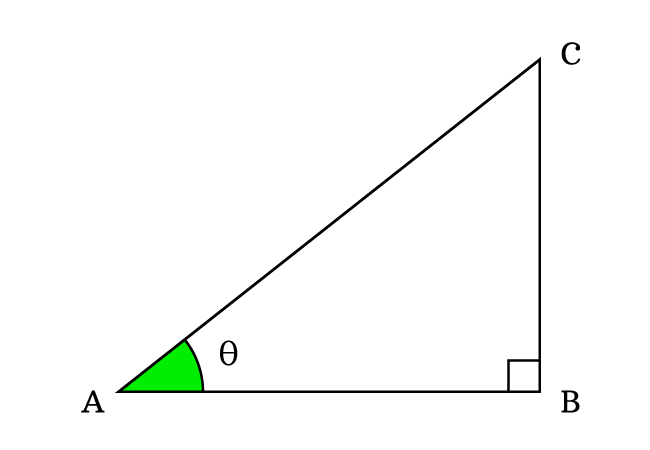
According to the definitions of the trigonometric functions, express the sine and cosine functions in ratio form at an angle theta.

$\sin{\theta} \,=\, \dfrac{BC}{AC}$

$\cos{\theta} \,=\, \dfrac{AB}{AC}$

Divide the Cosine by Sine function

Now, divide the cosine function by the sine function for evaluating the quotient of them.

$\dfrac{\cos{\theta}}{\sin{\theta}} \,=\, \dfrac{\dfrac{AB}{AC}}{\dfrac{BC}{AC}}$

$\implies$ $\dfrac{\cos{\theta}}{\sin{\theta}}$ $\,=\,$ $\dfrac{AB}{AC} \times \dfrac{AC}{BC}$

$\implies$ $\dfrac{\cos{\theta}}{\sin{\theta}}$ $\,=\,$ $\dfrac{AB}{BC} \times \dfrac{AC}{AC}$

$\implies$ $\dfrac{\cos{\theta}}{\sin{\theta}}$ $\,=\,$ $\dfrac{AB}{BC} \times \require{cancel} \dfrac{\cancel{AC}}{\cancel{AC}}$

$\implies$ $\dfrac{\cos{\theta}}{\sin{\theta}}$ $\,=\,$ $\dfrac{AB}{BC} \times 1$

$\implies$ $\dfrac{\cos{\theta}}{\sin{\theta}}$ $\,=\,$ $\dfrac{AB}{BC}$

Express the Ratio in Trigonometric function

We have derived in the above step that the ratio of cosine by sine is equal to the quotient of lengths of adjacent side ($AB$) by opposite side ($BC$).

$\dfrac{\cos{\theta}}{\sin{\theta}}$ $\,=\,$ $\dfrac{AB}{BC}$

According to the trigonometry, the quotient of $AB$ by $BC$ represents the cotangent. Here, the angle of right triangle is theta. Therefore, the cot function is written as $\cot{\theta}$.

$\,\,\,\therefore\,\,\,\,\,\,$ $\dfrac{\cos{\theta}}{\sin{\theta}}$ $\,=\,$ $\cot{\theta}$

Therefore, it is proved that the quotient of cosine function by sine function is equal to the cotangent function mathematically.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.