Equation of a Circle when the circle touches the x-axis

An equation that represents a circle when the circle touches the $x$-axis at a point is called the equation of a circle touching the $x$-axis.

Introduction

The circle touches the horizontal axis at a particular point in a special case and it can be written mathematically in an equation.

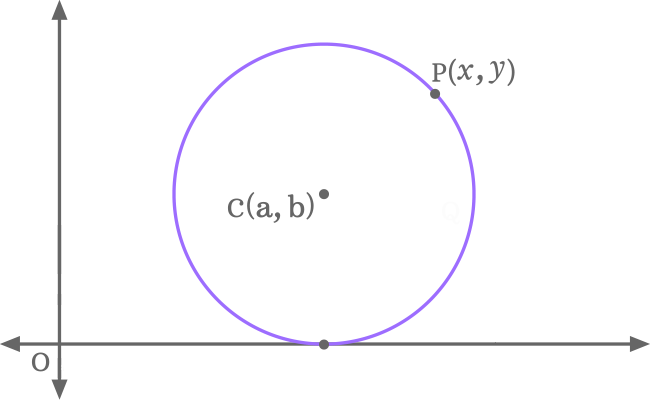
Let $C$ represents the centre of a circle and $P$ represents any point on its circumference. If the coordinates of the center are represented by $a$ and $b$, then the centre in coordinate form is written as $C (a, b)$.

Similarly, $P (x, y)$ represents a point on the circumference of the circle. In this case, the circle is touching the $x$-axis at a point and it can be expressed in a mathematical equation.

Simple form

$(x-a)^2+(y-b)^2 \,=\, b^2$

Expansion

$x^2+y^2\,-\,2ax\,\,–\,2by+a^2 \,=\, 0$

Alternative form

The above two equations are also written alternatively in the following two forms respectively if the coordinates of the center are represented by $h$ and $k$. It means, $C (h, k)$.

Simple form

$(x-h)^2+(y-k)^2 \,=\, k^2$

Expansion

$x^2+y^2\,-\,2hx\,\,–\,2ky+h^2 \,=\, 0$

Proof

Learn how to prove the equation of a circle when the circle touches the $x$ axis.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.