Chord

A line segment whose endpoints lie on a circle is called a chord of a circle.

Introduction

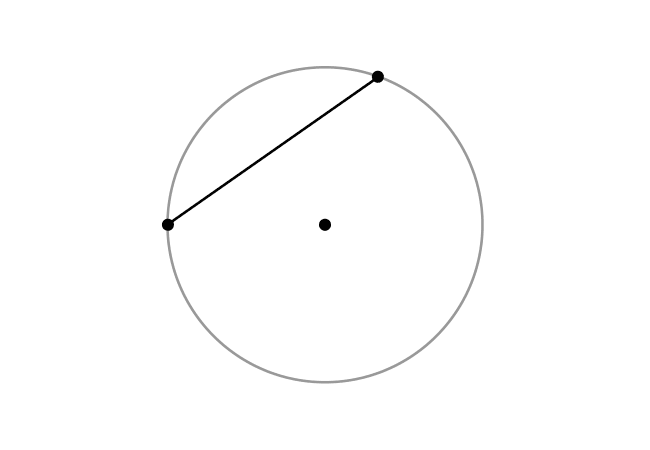
There are many points on any circle. In some cases, a point on a circle is connected with another point on the same circle by a straight line.

The two points on the circle become the endpoints of the straight line. Hence, the straight line is geometrically known as a line segment.

The same line segment connects the both points on the circle and it is called a chord of the circle in geometric mathematics.

Example

The concept of a chord of a circle can be understood from an understandable geometrical example.

Let $M$ and $N$ be any two points on a circle, and connect them by a straight line. The points $M$ and $N$ become the endpoints of line segment $\overline{MN}$ geometrically. So, the line segment $\overline{MN}$ is called a chord of this circle.

Similarly, $D$ and $E$ are another two points on the same circle but they are exactly opposite in the point view of the center (or centre) of the circle. The line segment $\overline{DE}$ is also called a chord of the circle.

Actually, the chord $\overline{DE}$ also represents the diameter of circle in this case. It clears that the line segment that represents the diameter is a longest chord of the circle.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.